同調回路3
共振回路の種類、同調周波数の説明です。
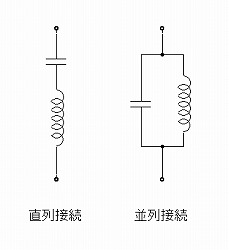
直列共振・並列共振
共振回路(同調回路)のインピーダンスとは、
回路図の端子(小さな丸印)から観測した値です。
同調回路はコンデンサーとコイルを使用しますが、この2つの部品は周波数に対するインピーダンス(交流電流の流れにくさ)が逆なのです。つまり、周波数が高い電流の場合、コンデンサーは流れやすく、コイルは流れにくい性質があります。表現を変えて再度説明すると、周波数が低い電流の場合、コンデンサーは流れにくく、コイルは流れやすい性質があるのです。
さて、コンデンサーとコイルを組み合わせ方(接続方法)には、直列と並列の2通りがあります。そして、使用したコンデンサーとコイルの値によって、ある1つの周波数だけ極端にインピーダンスが異なる特性が生じます(これは見方によっては、電気的な共振現象が生じたように観察されます)。この周波数を共振周波数と言います。
直列共振回路の特性は、ある1つの共振周波数の信号に対してインピーダンスがほぼ零になり、他の周波数の信号に対してはインピーダンスがほぼ無限大になります(低い周波数はコンデンサーが、高い周波数はコイルが電流を止める)。
逆に、並列共振回路の特性は、ある1つの共振周波数の信号に対してインピーダンスがほぼ無限大になり、他の周波数の信号に対してはインピーダンスがほぼ零になります(低い周波数はコイルを、高い周波数はコンデンサーを電流が通り抜ける)。
このように、コンデンサーとコイルの接続方法で「直列共振」と「並列共振」は区別され、逆のインピーダンス特性を持つことになります。
共振特性と同調回路の動作原理
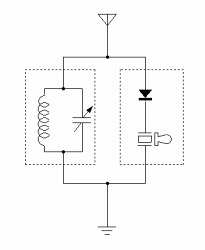
見慣れたゲルマラジオの回路図を書き直しています。
「検波&出力の直列回路」は同調回路と並列接続の関係。
周波数によって同調回路のインピーダンスは大きさが
変化することで、どちらへ信号が流れるか決まります。
さて、電流はインピーダンスが小さい、つまり抵抗が小さいと、より多く流れようとする性質があります(オームの法則)。 言い換えると、複数の電気回線が存在するとき、電流は抵抗の小さい回線を通過しようとする性質がある、と言えます。 もちろん、アンテナ回路から伝わってくる電気信号(電流)も同様で、通過しやすい箇所を流れようとします。
ゲルマラジオの場合、同調回路に並列共振を用いる例が多いです。 また、検波回路(ダイオード)と出力回路(イヤホン)は直列であり、この「検波&出力の直列回路」は同調回路と並列に接続される関係です。 「検波&出力の直列回路」もインピーダンス値を持っており、セラミックイヤホンを使うなら、5kΩなどの値を仮定できるでしょう。
この場合、共振周波数の信号がアンテナからアースへ流れようとする場合、 同調回路のインピーダンスがほぼ無限大のため、インピーダンスが相対的に低い「検波&出力の直列回路」へ電流が流れようとします。 この通過する電流によって音声信号を得ているのです。
逆に、共振周波数と異なる信号がアンテナからアースへ流れようとする場合、 同調回路のインピーダンスがほぼ零のため、共振回路の両端は、ショート状態になります。 このため、電流は同調回路側を通過し、インピーダンスが相対的に高い「検波&出力の直列回路」へ流れないのです。
同調周波数
コイルとコンデンサーの並列回路における合成インピーダンスZは、1/Z=1/(j2πfL)+j2πfC の立式から、Z=j2πfL/(1−(2πf)2LC) と変形、Zが無限大になる条件は、(2πf)2LC=1と求められます。 コイルとコンデンサーの直列回路における合成インピーダンスZは、Z=j2πfL+1/(j2πfC) と立式、Zがゼロになる条件は、j2πfL−j/(2πfC)=0ですから式を変形すると、(2πf)2LC=1と求められます。 したがって、直列共振と並列共振の共振周波数は、結果として同じ式になります。
同調周波数F(単位はHz、発音は「ヘルツ」)は、コンデンサーの容量C(単位F、発音は「ファラッド」)とコイルのインダクタンスL(単位H、発音は「ヘンリー」)によって、つぎのとおり計算できます。
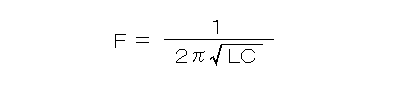 (1)
(1)ところで、受信の対象であるAM放送(中波放送)の周波数である531〜1602kHzに対して、同調コンデンサーは数百pF、同調コイルは数百μHを使用する例がほとんどです。
前記の式(1)は基本単位で関係を表現した式ですから、補助単位の計算が必要になると扱う桁数が多く、一般の電卓では計算が困難です。 そこで、周波数FをkHz、容量CをpF、インダクタンスLをμHと、扱う補助単位を定めて式を整理すると、計算の桁数を減らせるので一般のルート演算付き電卓でも計算できます。
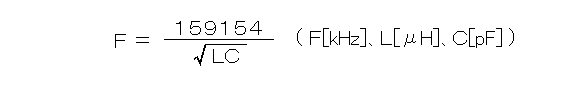 (2)
(2)共振周波数の計算
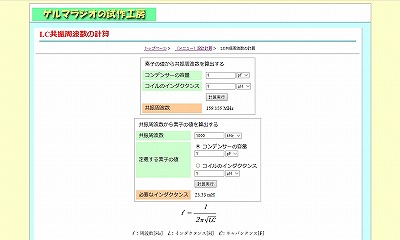
補助単位に慣れなくて式(1)の計算に自信が持てない方、ルート演算ができる電卓が手元になくて式(2)の計算もできない方がいらっしゃかと思います。そこで、周波数F、コンデンサーの容量C、コイルのインダクタンスLについて計算ができるページを当サイトで準備しました。LC共振周波数の計算で計算できます。