同調回路4
共振回路の性能評価に関する内容です。
共振回路の良さ
共振回路の良さ(quality of resonance)は、Qと呼ばれる数値(単位を持たない無次元数)で表します。
Qの定義を表現すると、
 (1)
(1)
であり、Qを求める具体的な計算式は、直列共振回路、並列共振回路のいずれも、
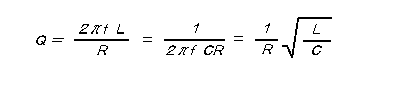 (2)
(2)
になります(f、L、C、Rの数値は全て基本単位)。
Qが高いほど高性能だと見なされていますが、Qの値は回路の目的に応じた値であることが大切です。
Qを求める式には共振エネルギーを損失する要素として、抵抗成分Rを含んでいます。 共振回路には特別な理由がない限り、電子パーツとして抵抗器を加えません。 しかし、実際にはコイル、コンデンサの本体自身やそのリード線、接続に使用した配線等に抵抗成分が存在します。 この様子を表すため、等価回路(実物の部品そのものではなく、ピュアな電気的特性の表現を意図した回路)と称して、共振回路に抵抗器の記号を追加します。 抵抗成分の構成ですが、現実には、ほとんどがコイルを形成している導線の高周波抵抗、つまり、コイルの実効抵抗が占めています。
Qの意味
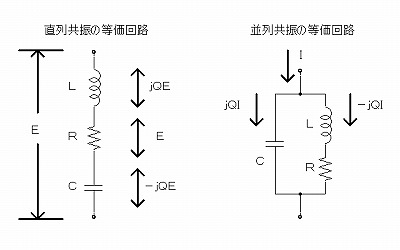
( jは位相が90度進んでいることを、-jは位相が90度遅れていることを表示 )
まず、Qが意味する共振回路の特性として、直列共振回路では電圧が、並列共振回路では電流が、Q倍になることを表します。 つまり、直列共振回路に外部からE[V]を加えると、素子の両端にQE[V]が発生し、並列共振回路に外部からI[A]を加えると、素子にQI[A]が流れることになります。
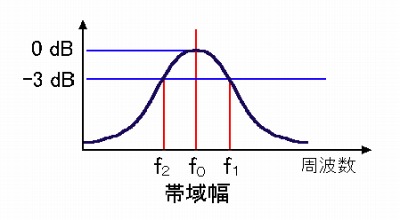
共振特性と帯域幅、Qの関係
また、共振回路のQは、周波数の選択度を表します。
共振周波数f0で共振した際、直列共振回路では素子の両端電圧QEを、並列共振回路では素子に流れる電流QIを基準(0dB)とします。
この際、共振周波数f0に対して上下の周波数で、値が−3dB(基準値の1/√2=0.707倍)となる周波数(f1、f2)が存在します。
これらの周波数とQには、
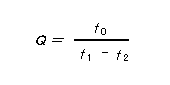 (3)
(3)
の関係があります。 f1-f2 は特に、帯域幅と呼ばれています。
つまり、帯域幅が狭いほどQは高くなり、共振周波数f0以外の信号が紛れ込まないことになります。
以上、Qを大雑把に表現すると「どれくらい強く、鋭く共振できるかを表した値」と言ったところでしょうか。
コイルのQ
ところで、共振エネルギーを損失する要素Rは、コンデンサーの状態や配線状況が良い場合は、コイルの実効抵抗でほとんどを占めています。 すなわち、コイルの性能が共振回路のQに、大きく関与していると言えます。 そこで、コイルの性能を示すため「コイルのQ」という言葉が使われていますが、多くの場合、共振回路のQをコイルのQと呼び変えているに過ぎません。 損失Rはコイルに由来する値であると考えれば、式(2)における左側の式は、コイルのファクターと周波数だけでQを表現しています。
コイルの実効抵抗Rは固定値ではなく、周波数によって値が変化します。 これは、コイルの線材で生じる表皮効果や誘電損が、扱う周波数によって異なるためです。 コイルのQ(共振回路のQ)は周波数によって変化する値なので、正しく評価するには、使用する周波数の交流でQ値を測定する必要があります。
コイルのQを求める理論式で周波数を考慮したRを含む式があると便利ですが、どのような形態のコイルでも計算対象とする万能な式は存在せず、コイルの形状や巻き方など、特定の条件下で適用できる式しか存在しないようです。 Qを求めるには実測するのが良いようです。
ゲルマラジオに必要なQ
ここで、ゲルマラジオの高性能化を考えると、同調回路のQが高いほど、感度と選択度が高くなります。 Qを高くするには、実効抵抗RとCを小さく、Lを大きくすれば良いことが、式(2)から分かります。 しかし、簡単にHi-Qは得られません。 R、C、Lの三者は、どれかを良くしようとすると、他が悪くなるトレードオフ的な性質を帯びているからです。 例えば、Lを大きくするために、同調コイルの巻数を増やすと、線材が長くなることで実効抵抗Rが増加し、線材が隣り合う回数が増えて浮遊容量Cも増加します。 そこで、Cを減らそうと巻き方を工夫(ハニカム巻、スパイダー巻等)することになりますが、これだけではRは減少しません。
このパズル的な問題に対し、多くの先人がチャレンジされ、色々なデータを残してくれており、その一部はインターネット上にも公開されています。 これらを真似て製作するだけで、十分実用的なQを持つゲルマラジオが完成します。 しかし、まだまだ検討の余地が大いに残っているハズです。 色々なアイデアと工夫で製作するコイルのHi-Qクエスト、案外面白いですよ。
【参考】 Qメーター構成品の試作