Qメーター構成品の試作
ゲルマラジオの高性能化を検討すると、コイルのQは検討事項の一つになります。Qの専用測定器はQメーターと呼ばれており、おおまかな仕組みは、高周波信号を計測用の共振回路に加えて電圧測定を行っています(直列共振法)。自作したコイルを自作のQメーターで測定するのも、面白そうです。
今回の試作品は、Qメーターの構成に必要な高周波の信号源と計測用の共振回路を、1つのケースに収めたものです。製作のハードルを下げるため、電圧測定は外付けで、メーカー製の測定器に任せるほか、キットも活用したいと思います。
MAX038
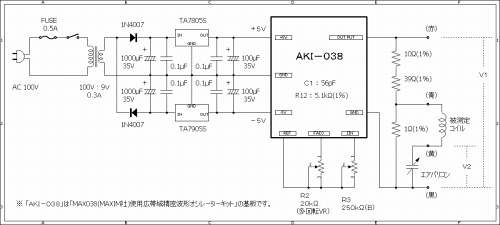
高周波の信号源(発振回路)には(株)秋月電子通商の「MAX038使用広帯域精密波形オシレータキット」(通販コード K-00187)を利用します。MAX038は0.1Hz〜20MHzの出力が可能ですが、このキットではコンデンサC1を切り換えることで9レンジに分けて選択するように設計されています。また、出力波形の切換え(正弦波、方形波、三角波)、デューティサイクルの可変(15〜85%)も可能です。Q測定用の高周波オシレータとして利用するに当たり、キットに同梱されていたデータシートを参照し、おおよそ100kHz〜10MHzをレンジ切替なしで連続カバーできるように部品定数などを変更(C1、R2、R3、R12)、波形は正弦波、デューティサイクル50%固定に設定します。
キットは±5V各100mAの正負電源が必要なので、三端子レギュレーターで供給します。発振防止用の0.1μFは念のため、三端子レギュレーターと短く接続したいので、基板の裏側で結線しました。
計測用の共振回路にはエアバリコンを使い、バーニアダイヤルで調整しやすくします。エアバリコンの極板が錆びていたり、埃などで汚れていなければ、測定されるQはコイルのQと見なして良いだろうと期待されます。

Qメーター構成品の外観

Qメーター構成品の内部状況

背面に電源スイッチ、ヒューズターミナルを配置。ACコードは抜け止めに結び、
被覆が傷まないよう、ゴムブッシュを利用します。

電源基板の様子。発振防止用の0.1μFは4個とも、基板裏で
三端子レギュレーターの足元に短く結線しています。

AKI-038基板はキットの説明書に従い、PLL化しない場合の加工を施し、
必要な部品だけをはんだ付けしています。

AKI-038基板からジョンソンターミナルまでは、
同軸ケーブル(1.5D2V)を使っています。
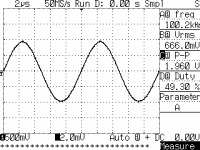
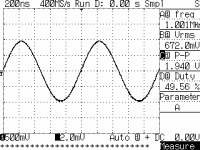
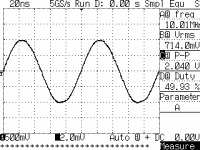
動作を確認したところ、MAX038のIIN(周波数調整)によって180kHz〜7.5MHzまで可変しました。FADJ(周波数微調整)を併用すると、IINの下限で45kHz〜330kHz、IINの上限で3.2MHz〜11.9MHzまで可変します。都合、45kHz〜11.9MHzにおけるQ値の測定が出来そうです。
Qの算出方法
Qメーターであればメーターの指示値が即、Q値を表しますが、ここでは測定の原理に従って計算によって求めます。試作品の電圧測定と周波数の確認には、ユニバーサルカウンタやオシロスコープなどを利用します。以下の測定手順でQを算定します。
1 高周波オシレータの出力を測定したい周波数F(例えば1000kHz)にセットする。
2 バリコンを操作して周波数F に共振させる。つまり、バリコンの両端電圧(V2)が最大となるように調整する。
3 共振した状態のまま、高周波信号源の電圧(V1)を測定する。
4 抵抗器で分圧しているので、共振回路の両端電圧はV3=V1/50
5 以上の計測から、Q=V2/V3=(V2/V1)×50
フリーウェアソフトでQを算出
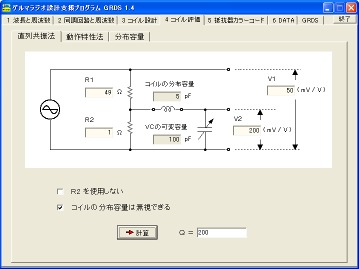
直列共振法によるQの計算画面(GRDS Version1.4)
拙作のフリーウェアソフト「GRDS」では、Ver1.2以降で上記の計算に対応しています。説明やダウンロードについては、GRDSインフォメーション(外部サイト)をご覧下さい。
市販バーアンテナの測定例
構築したQ測定システムでバーアンテナのQを測定しました。製品に同梱されていた説明書のとおり、100以上のQを測定することができました。
測定中のコイルとそのリード線は、できるだけ周囲から離し、位置も変更しないようにします。

測定中のコイルは、周囲の影響を受けないように気をつけます。
プラスチックで机から少し持ち上げるだけでも効果があります。
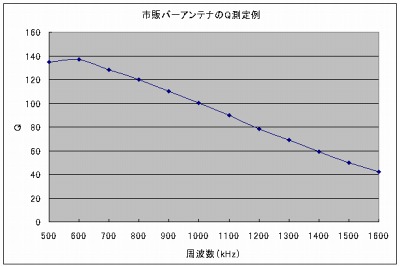
市販バーアンテナのQ測定結果
回路定数の改訂
本試作品は、広い周波数範囲でQを測定できる点では良いのですが、ゲルマラジオと言えばやはり中波がメインであり、オーバースペックとも言えます。改めて中波専用のQメーターを検討していたところ、回路定数の配慮が不足していることに気付きました。被測定コイルとエアバリコンで構成した直列共振回路は、共振時の実効抵抗値がとても小さい値になります。200μHと360μHの実効抵抗値を計算してみました。(表内の単位はオーム)
| Q | 200μH | 360μH | ||||
|---|---|---|---|---|---|---|
| 500 kHz | 1000 kHz | 1500 kHz | 500 kHz | 1000 kHz | 1500 kHz | |
| 10 | 62.8 | 125.7 | 188.5 | 113.1 | 226.2 | 339.3 |
| 50 | 12.6 | 25.1 | 37.7 | 22.6 | 45.2 | 67.9 |
| 100 | 6.3 | 12.6 | 18.8 | 11.3 | 22.6 | 33.9 |
| 200 | 3.1 | 6.3 | 9.4 | 5.7 | 11.3 | 17.0 |
| 300 | 2.1 | 4.2 | 6.3 | 3.8 | 7.5 | 11.3 |
| 400 | 1.6 | 3.1 | 4.7 | 2.8 | 5.7 | 8.5 |
| 500 | 1.3 | 2.5 | 3.8 | 2.3 | 4.5 | 6.8 |
| 600 | 1.0 | 2.1 | 3.1 | 1.9 | 3.8 | 5.7 |
| 700 | 0.9 | 1.8 | 2.7 | 1.6 | 3.2 | 4.8 |
| 800 | 0.8 | 1.6 | 2.4 | 1.4 | 2.8 | 4.2 |
| 900 | 0.7 | 1.4 | 2.1 | 1.3 | 2.5 | 3.8 |
| 1000 | 0.6 | 1.3 | 1.9 | 1.1 | 2.3 | 3.4 |
Qが高いほど、インダクタンスが小さいほど、コイルの実効抵抗値は小さくなります。この実効抵抗値と1Ωの抵抗器を並列にするとどうでしょう? 合成抵抗値は1Ωから大きく変化することで、49Ωとの組合せで定義する分圧比に影響を与え、直列共振回路に印加される電圧が低下します。本来なら49:1で一定である分圧比の理論値に対し、どれだけの誤差が生じるか、Qが300の場合における計算結果をグラフ化しました。
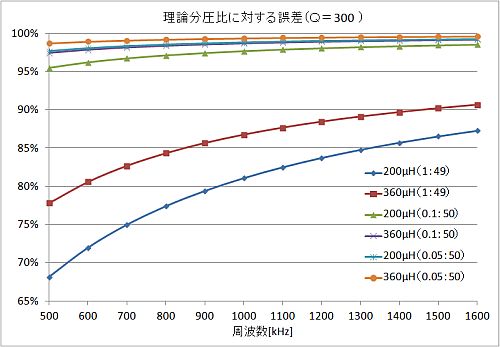
200μH(0.05:50)と360μH(0.1:50)は、誤差がほぼ同じためグラフが重なっています。
分圧比の誤差はQ値の誤差になります。1Ωと49Ωで分圧してQが300の200μHを測定しようとした場合、700kHzで本来より約25%低下したQ値の計算結果を得てしまうことになります。ここで直列共振回路と並列にする抵抗値を0.05Ωまで小さくして、50Ωと組み合わせて分圧すると、誤差は3%以内に収まります。
本試作品で使用したキットの出力インピーダンスは50Ωであることから、分圧を行う抵抗器について、10Ω(1%)と39Ω(1%)の直列を100Ω(0.1%)2本の並列に変更し、1Ω(1%)を0.05Ω(1%、無誘導)に変更することにしました。
(2012/11/11 本章追記)

(改訂前)10Ωと39Ωの直列で49Ωを得て、1Ωと分圧している。

(改訂後)100Ω2本の並列で50Ωを得て、0.05Ωと分圧している。